Skip to main content

2125. Number of Laser Beams in a Bank

題目​

完整題目

Anti-theft security devices are activated inside a bank. You are given a 0-indexed binary string array bank representing the floor plan of the bank, which is an m x n 2D matrix. bank[i]represents the ithi^{th} row, consisting of '0's and '1's. '0' means the cell is empty, while'1' means the cell has a security device.

There is one laser beam between any two security devices if both conditions are met:

The two devices are located on two different rows: r1r_1 and r2r_2, where r1r_1 < r2r_2. For each row i where r1r_1 < i < r2r_2, there are no security devices in the ithi^{th} row. Laser beams are independent, i.e., one beam does not interfere nor join with another.

Return the total number of laser beams in the bank.

Example 1

1

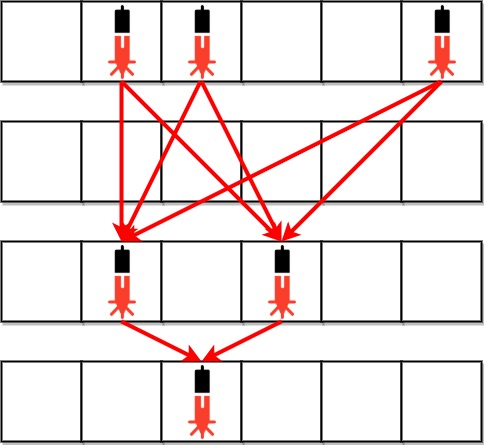
Input: bank = ["011001","000000","010100","001000"]
Output: 8
Explanation: Between each of the following device pairs, there is one beam. In total, there are 8 beams:
 * bank[0][1] -- bank[2][1]
 * bank[0][1] -- bank[2][3]
 * bank[0][2] -- bank[2][1]
 * bank[0][2] -- bank[2][3]
 * bank[0][5] -- bank[2][1]
 * bank[0][5] -- bank[2][3]
 * bank[2][1] -- bank[3][2]
 * bank[2][3] -- bank[3][2]
Note that there is no beam between any device on the 0th row with any on the 3rd row.
This is because the 2nd row contains security devices, which breaks the second condition.

Exmaple 2

2

Input: bank = ["000","111","000"]
Output: 0
Explanation: There does not exist two devices located on two different rows.

Constraints

  • m == bank.length
  • n == bank[i].length
  • 1 \<= m, n \<= 500
  • bank[i][j] is either '0' or '1'.

題目難易度​

Medium

解題想法​

題目基本上就是要找有多少條雷射。我們只需要找出每一層可以有幾個發射點，再去除掉沒有發射點的層數，兩層兩層去看（相乘），就可以知道每兩層有幾條雷射。

初試​

Runtime: 102ms, 32.94%

Memory Usage: 52.6MB, 20%

  • m 代表 bank 的長度，n 代表 bank 每個 row 的長度
  • 時間複雜度：O(m∗n)O(m * n)
  • 空間複雜度：O(1)O(1)
/**
 * @param {string[]} bank
 * @return {number}
 */
var numberOfBeams = function (bank) {
  const res = [];
  for (let e of bank) {
    const count = e.split("").filter((e) => e === "1").length;
    if (count !== 0) res.push(count);
  }

  let r = 0;
  for (let i = 1; i < res.length; i++) {
    r += res[i - 1] * res[i];
  }

  return r;
};