2482. Difference Between Ones and Zeros in Row and Column

題目

完整題目

You are given a 0-indexed m x n binary matrix grid.

A 0-indexed m x n difference matrix diff is created with the following procedure:

• Let the number of ones in the $i^{th}$ row be $onesRow_i$.
• Let the number of ones in the $j^{th}$ column be $onesCol_j$.
• Let the number of zeros in the $i^{th}$ row be $zerosRow_i$.
• Let the number of zeros in the $j^{th}$ column be $zerosCol_j$.
• $diff[i][j]$ = $onesRow_i$ + $onesCol_j$ - $zerosRow_i$ - $zerosCol_j$

Return the difference matrix diff.

Example 1

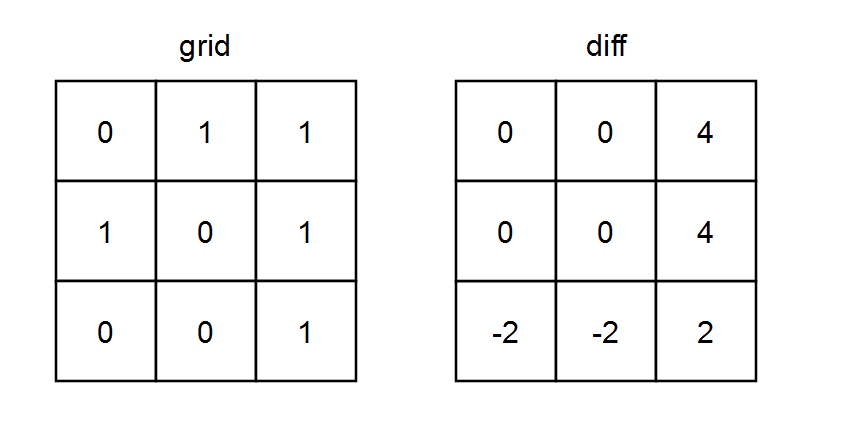
Input: grid = [[0,1,1],[1,0,1],[0,0,1]]
Output: [[0,0,4],[0,0,4],[-2,-2,2]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 2 + 1 - 1 - 2 = 0
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 2 + 1 - 1 - 2 = 0
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 2 + 3 - 1 - 0 = 4
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 2 + 1 - 1 - 2 = 0
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 2 + 1 - 1 - 2 = 0
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 2 + 3 - 1 - 0 = 4
- diff[2][0] = onesRow2 + onesCol0 - zerosRow2 - zerosCol0 = 1 + 1 - 2 - 2 = -2
- diff[2][1] = onesRow2 + onesCol1 - zerosRow2 - zerosCol1 = 1 + 1 - 2 - 2 = -2
- diff[2][2] = onesRow2 + onesCol2 - zerosRow2 - zerosCol2 = 1 + 3 - 2 - 0 = 2

Example 2

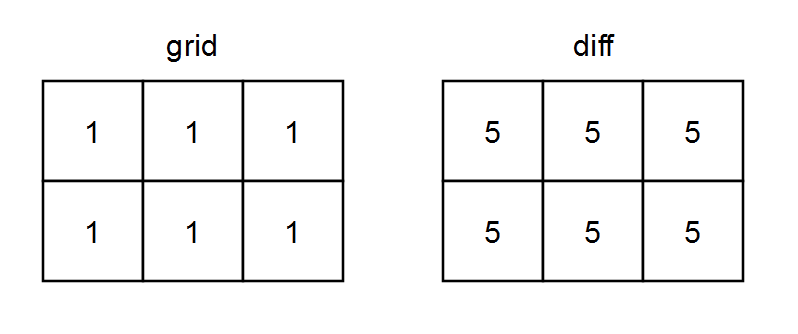
Input: grid = [[1,1,1],[1,1,1]]
Output: [[5,5,5],[5,5,5]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5

Constraints

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• grid[i][j] is either 0 or 1.

題目難易度

Medium

解題想法

第一眼的想法是先把每一個 row 和 colume 的 0 和 1 的次數先算出來，再用一個 Map 去紀錄。最終再把題目的二維陣列跑過一次，去 Map 查值並做加減。

初試

Runtime: 646ms, 6.82%

Memory Usage: 182MB, 6.82%

• 時間複雜度：$O(m+n+(m*n))$
• 空間複雜度：$O(1+m+n)$

/**
 * @param {number[][]} grid
 * @return {number[][]}
 */
var onesMinusZeros = function (grid) {
  const x = new Map();

  for (let i = 0; i < grid.length; i++) {
    const zero = grid[i].filter((x) => x === 0).length;
    x.set(`r${i}zero`, zero);
    x.set(`r${i}one`, grid[i].length - zero);
  }

  for (let j = 0; j < grid[0].length; j++) {
    const one = grid.reduce((acc, val) => acc + val[j], 0);
    x.set(`c${j}zero`, grid.length - one);
    x.set(`c${j}one`, one);
  }

  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[0].length; j++) {
      grid[i][j] =
        x.get(`r${i}one`) +
        x.get(`c${j}one`) -
        x.get(`r${i}zero`) -
        x.get(`c${j}zero`);
    }
  }

  return grid;
};